Lower bound (time) on approximate agreement in shared memory
Algorithm
Consider an asynchronous shared memory model with single write registers and no process failures. Approximate agreement between \(n\) processes is the problem of agreeing \(n\) output values within \(\epsilon\) of each other, and all falling in the interval \([\min(\mathcal{I}), \max(\mathcal{I})]\), where \(\mathcal{I}\) is a set of input values assigned 1-1 to processes.
Result and proof
Any solution with input values in \( \{ 0, 1\} \) and \(\epsilon < 1 \) that provides obstruction freedom (each process will finish if it is scheduled for sufficiently many consecutive steps) has time complexity at least \(n\).
Proof: suppose for contradiction suppose it’s possible in less than \(n\) steps. Take two solo executions \(\sigma_i\) and \(\sigma_j\) of \(P_i\) and \(P_j\), starting at states (configurations) \(C_i\) and \(C_j\). In \(C_i\) all input values are \(0\), and in \(C_j\) all input values are \(1\) . \(P_i\) and \(P_j\) will output \(0\) and \(1\). Both \(P_i\) and \(P_j\) cannot distinguish \(C_i\) and \(C_j\) from a starting point \(C\), where \(P_i\) is given input \(0\) and \(P_j\) is given \(1\).
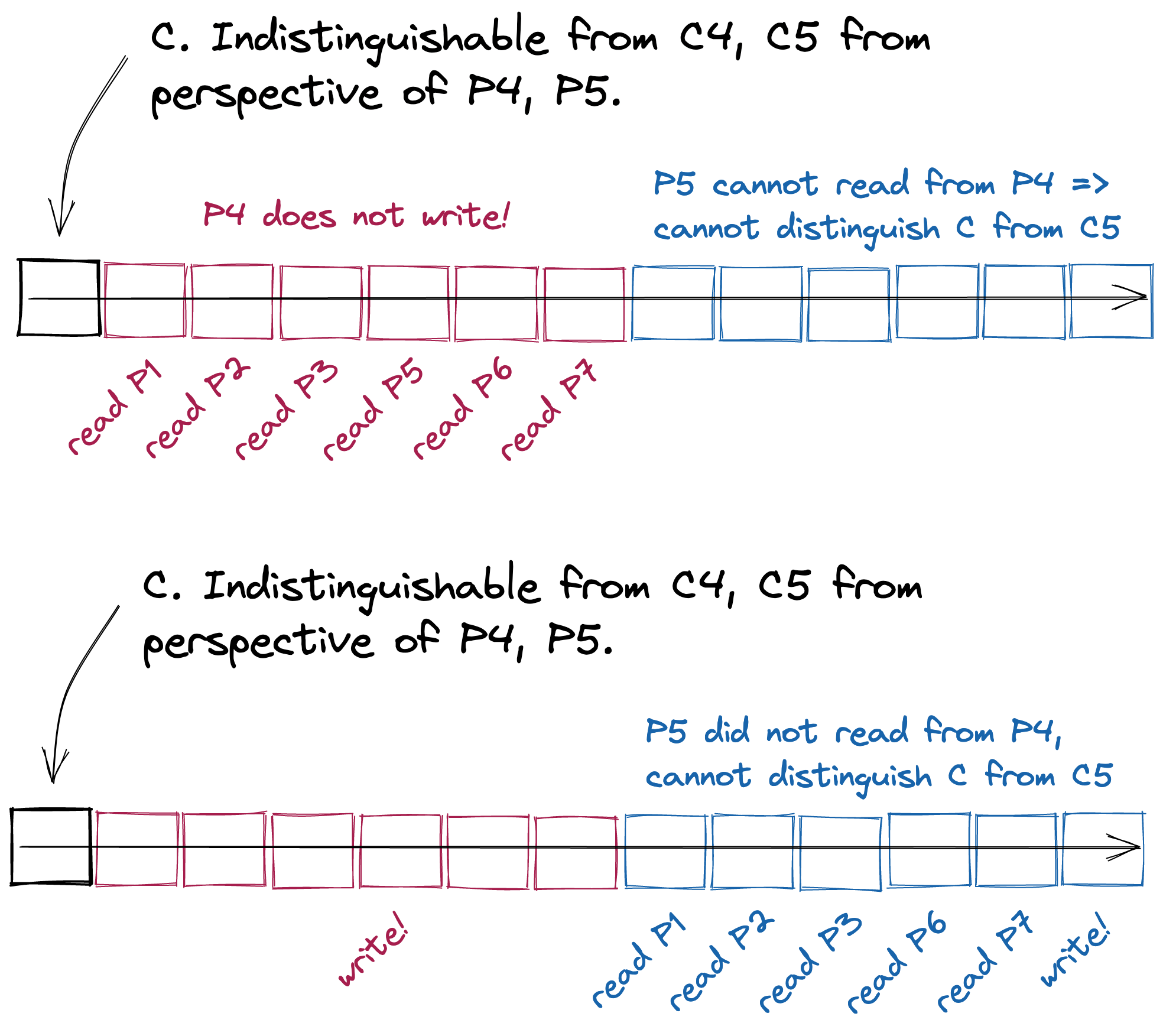
Moreover, in any execution a process does not have time to read the register of all other processes and write to its own register. This at least one of \(P_i\) and \(P_j\) will not have time to distinguish \(C_i\) (\(C_j\)) from \(C\). To see this, without loss of generality, if \(P_i\) does not read from \(P_j\) during \(\sigma_i\) then the execution \(\sigma_j\sigma_i\), starting from \(C\), will not be valid. If \(P_i\)does read from \(P_j\), but does not write to its own register, then \(P_j\) cannot distinguish \(C\) and the state after running \(\sigma_i\) from \(C\). Therefore, starting from \(C\), \(\sigma_i\sigma_j\) will not be valid □
