Lower bound (space) on FIFO mutual exclusion in shared memory
Algorithm
Mutual exclusion algorithms have four stages and satisfy some conditions. The four stages are the entry, critical section, exit and remainder. The entry acquires the resource, the critical section uses it and the exit releases it. When a process does not care about the resource, it is in the remainder. The algorithm must satisfy
- at most one process is in the critical section at a time
- starting from any state where some process is in the entry, some process always enters the critical section eventually (deadlock freedom)
- a process can always perform the exit in a finite number of its own steps only (unobstructed exit)
Additionally, FIFO algorithms have a doorway at the start of the entry. Processes are guaranteed to enter the critical section in the same order that they complete the doorway. A doorway can always be completed by a process in a finite number of its own steps only.
Result and proof
In an asynchronous shared memory model with no process failures, implementing FIFO mutual exclusion for n processes requires log(n) bits of space. That is, at least n values must be able to be stored, one for each process.
Proof: for contradiction, suppose it’s possible with fewer than log(n) bits. Suppose also an adversarial scheduler who schedules processes in round robin order. Let C(0) be a state where all processes are in the remainder section. For i in 0..(n-1) let C(i+1) be a state where P(i) completes the doorway. In this way, in C(i), each process 0..(i-1) has completed the doorway and rests in the entry.
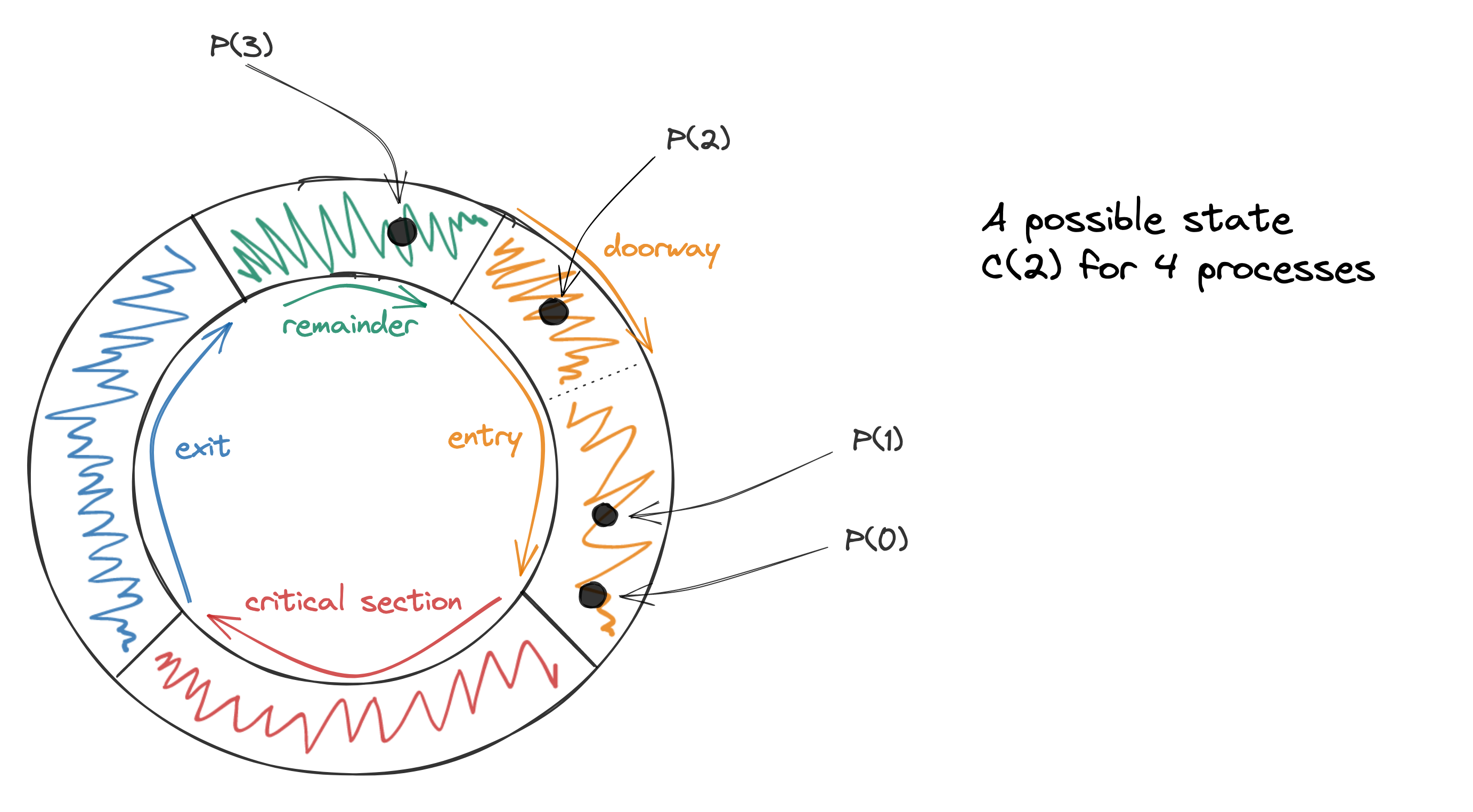
Starting from C(i), let σ be the sequence of events where processes 0..(i-1) are repeatedly scheduled until a process k in 0..(i-1) enters the critical section twice. By the pigeonhole principle there is a state C(j), i < j, indistinguishable from C(i). In C(j), P(i) has entered completed the doorway.
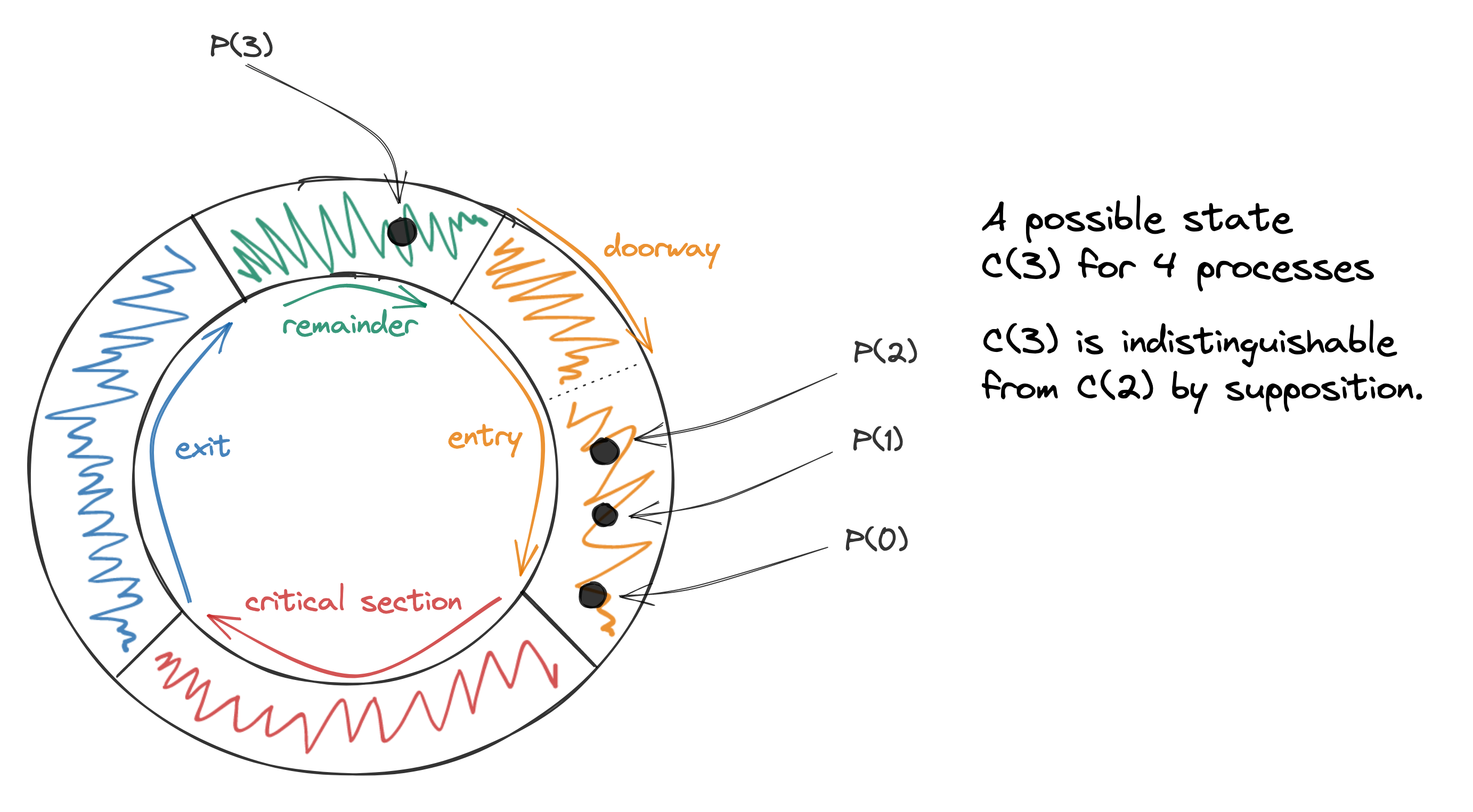
It is possible to schedule σ starting from C(j) instead of C(i), because they are indistinguishable, and in this execution P(k) will enter the critical section a second time, even though P(i) had previously entered the doorway and did not reach the critical section. This contradicts the FIFO property □
